https://www.acmicpc.net/problem/2225
2225번: 합분해
첫째 줄에 답을 1,000,000,000으로 나눈 나머지를 출력한다.
www.acmicpc.net
합분해 문제이다.
해당 문제를 이해하기 위해서 간단한 예시를 들어보자.
만약 N = 4, K= 2 인 경우를 생각해보자.
그럼 숫자 4를 0~4 의 숫자로 두개를 합해서 만들어야 하는 경우의 수를 구하면 된다.
그럼 아래와 같은 순서쌍이 나오게 된다.
(0,4), (4,0), (3,1), (1,3), (2,2)
위와 같이 5개의 순서쌍이 나와서 5개가 답이된다.
그럼 이제 일반화 가정을 거쳐보자.
(0,4), (4,0), (3,1), (1,3), (2,2)
위와 같이 순서쌍을 뽑는다고 가정했을 경우에
4 = x + r
이라고 볼 수 있다.
여기서 x 와 r 의 관계는 x 가 정해지면 r은 자연스럽게 정해진다고 생각하면 편하다.
그래서 위의 순서쌍에 빨간표시를 해둔것을 본다면
0을 선택하면 자연스럽게 4가 정해지고, 4를 택하면 자연스럽게 0이 정해지는 것이다.
즉 점화식을 사용하여 일반화 시켜보면 아래와 같다.
dp[K][N] = dp[K-1][0] + dp[K-1][1] + ... + dp[K-1][N]
위의 점화식을 해석해보면 0~N 까지의 숫자 K 개로 N 을 만들때,
dp[K-1][0] 은 0을 선택하는 경우고
dp[K-1][1] 은 1을 선택하는 경우라고 생각하면 된다.
그리고 논리적으로 dp[0][i] (i ∈ (0,1,2,...,N)) 은 무조건 0이 된다.
왜냐하면 0개로 N 을 만들수 있는 방법은 0이기 때문이다.
dp[1][i] (i ∈ (0,1,2,...,N)) 는 무조건 1이 된다.
0 ~ N 숫자중에 하나를 뽑아서 N 을 만드는 방법은 한가지 뿐이기 때문이다.
dp[i][0] (i ∈ (0,1,2,...,K)) 또한 1이다. 0 을 만드는 방법은 0 하나를 택하는 방법 하나뿐이기 때문이다.
N = 4, K = 2 일때의 경우를 생각해보자. (dp[K][N] 기준이다.)
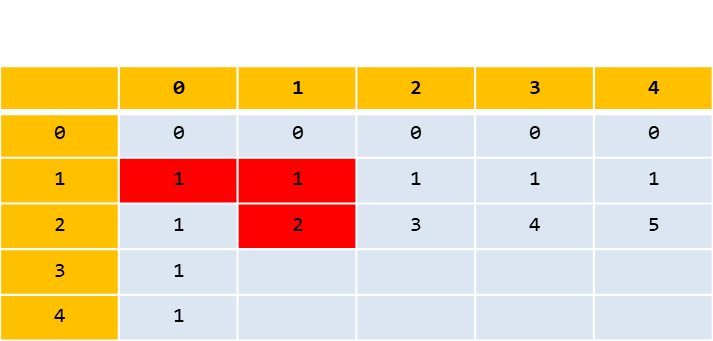
dp[2][1] = dp[1][0] + dp[1][1]
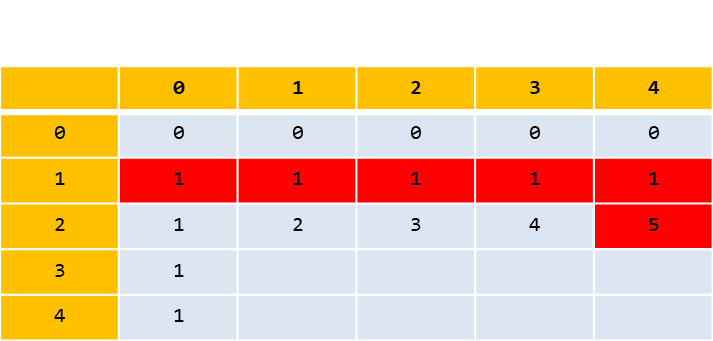
dp[2][4] = dp[1][0] + dp[1][1] + dp[1][2] + dp[1][3] + dp[1][4]
1. C++ 를 이용한 풀이
#include <iostream>
using namespace std;
int N,K;
long dp[201][201];
long DIV = 1000000000;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> N >> K;
dp[0][0] = 1;
for (int i = 1; i <= K; i++) {
for (int j = 0; j <= N; j++) {
for (int k = 0; k <= j; k++) dp[i][j] += dp[i-1][k];
dp[i][j] %= DIV;
}
}
cout << dp[K][N];
return 0;
}
2. JAVA 를 이용한 풀이
import java.io.*;
import java.util.*;
public class Main {
static int N,K;
static long DIV = 1000000000;
static long[][] mat;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer stk = new StringTokenizer(br.readLine());
N = Integer.parseInt(stk.nextToken());
K = Integer.parseInt(stk.nextToken());
mat = new long[K+1][N+1];
mat[0][0] = 1;
for (int i = 1; i <= K; i++) {
for (int j = 0; j <= N; j++) {
for (int k = 0; k <= j; k++) mat[i][j] += mat[i-1][k];
mat[i][j] %= DIV;
}
}
bw.write(mat[K][N] + "");
bw.close();
br.close();
}
}
그런데 위와 같은 알고리즘 말고 다른 알고리즘도 생각해 볼 수 있다.
dp[K][N] = dp[K-1][0] + dp[K-1][1] + ... + dp[K-1][N-1] + dp[K-1][N]
인데 dp[K-1][0] + dp[K-1][1] + ... + dp[K-1][N-1] = dp[K][N-1] 이라고 볼 수 있다.
즉, dp[K][N] = dp[K][N-1] + dp[K-1][N] 로 일반화 시킬 수 있다.
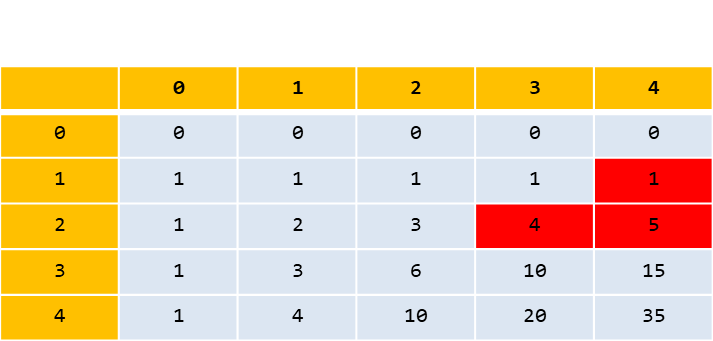
위의 알고리즘을 만들어보면 아래와 같다.
#include <iostream>
using namespace std;
int N,K;
long dp[201][201];
long DIV = 1000000000;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> N >> K;
for (int i = 1; i <= K; i++) dp[i][0] = 1;
for (int i = 0; i <= N; i++) dp[1][i] = 1;
for (int i = 1; i <= K; i++) {
for (int j = 1; j <= N; j++) {
long sum = dp[i][j-1] + dp[i-1][j];
dp[i][j] = sum % DIV;
}
}
cout << dp[K][N];
return 0;
}'코딩 테스트' 카테고리의 다른 글
| [백준] 1915번 - 가장 큰 정사각형 (4) | 2023.07.09 |
|---|---|
| [백준] 2240번 - 자두나무 (0) | 2022.10.01 |
| 백준 1937번 - 욕심쟁이 판다 (1) | 2022.08.30 |
| 백준 18223번 - 민준이와 마산 그리고 건우 (0) | 2022.05.24 |
| 백준 1854번 - K번째 최단경로 찾기 (0) | 2022.05.11 |
https://www.acmicpc.net/problem/2225
2225번: 합분해
첫째 줄에 답을 1,000,000,000으로 나눈 나머지를 출력한다.
www.acmicpc.net

합분해 문제이다.
해당 문제를 이해하기 위해서 간단한 예시를 들어보자.
만약 N = 4, K= 2 인 경우를 생각해보자.
그럼 숫자 4를 0~4 의 숫자로 두개를 합해서 만들어야 하는 경우의 수를 구하면 된다.
그럼 아래와 같은 순서쌍이 나오게 된다.
(0,4), (4,0), (3,1), (1,3), (2,2)
위와 같이 5개의 순서쌍이 나와서 5개가 답이된다.
그럼 이제 일반화 가정을 거쳐보자.
(0,4), (4,0), (3,1), (1,3), (2,2)
위와 같이 순서쌍을 뽑는다고 가정했을 경우에
4 = x + r
이라고 볼 수 있다.
여기서 x 와 r 의 관계는 x 가 정해지면 r은 자연스럽게 정해진다고 생각하면 편하다.
그래서 위의 순서쌍에 빨간표시를 해둔것을 본다면
0을 선택하면 자연스럽게 4가 정해지고, 4를 택하면 자연스럽게 0이 정해지는 것이다.
즉 점화식을 사용하여 일반화 시켜보면 아래와 같다.
dp[K][N] = dp[K-1][0] + dp[K-1][1] + ... + dp[K-1][N]
위의 점화식을 해석해보면 0~N 까지의 숫자 K 개로 N 을 만들때,
dp[K-1][0] 은 0을 선택하는 경우고
dp[K-1][1] 은 1을 선택하는 경우라고 생각하면 된다.
그리고 논리적으로 dp[0][i] (i ∈ (0,1,2,...,N)) 은 무조건 0이 된다.
왜냐하면 0개로 N 을 만들수 있는 방법은 0이기 때문이다.
dp[1][i] (i ∈ (0,1,2,...,N)) 는 무조건 1이 된다.
0 ~ N 숫자중에 하나를 뽑아서 N 을 만드는 방법은 한가지 뿐이기 때문이다.
dp[i][0] (i ∈ (0,1,2,...,K)) 또한 1이다. 0 을 만드는 방법은 0 하나를 택하는 방법 하나뿐이기 때문이다.
N = 4, K = 2 일때의 경우를 생각해보자. (dp[K][N] 기준이다.)

dp[2][1] = dp[1][0] + dp[1][1]

dp[2][4] = dp[1][0] + dp[1][1] + dp[1][2] + dp[1][3] + dp[1][4]
1. C++ 를 이용한 풀이
#include <iostream>
using namespace std;
int N,K;
long dp[201][201];
long DIV = 1000000000;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> N >> K;
dp[0][0] = 1;
for (int i = 1; i <= K; i++) {
for (int j = 0; j <= N; j++) {
for (int k = 0; k <= j; k++) dp[i][j] += dp[i-1][k];
dp[i][j] %= DIV;
}
}
cout << dp[K][N];
return 0;
}
2. JAVA 를 이용한 풀이
import java.io.*;
import java.util.*;
public class Main {
static int N,K;
static long DIV = 1000000000;
static long[][] mat;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer stk = new StringTokenizer(br.readLine());
N = Integer.parseInt(stk.nextToken());
K = Integer.parseInt(stk.nextToken());
mat = new long[K+1][N+1];
mat[0][0] = 1;
for (int i = 1; i <= K; i++) {
for (int j = 0; j <= N; j++) {
for (int k = 0; k <= j; k++) mat[i][j] += mat[i-1][k];
mat[i][j] %= DIV;
}
}
bw.write(mat[K][N] + "");
bw.close();
br.close();
}
}
그런데 위와 같은 알고리즘 말고 다른 알고리즘도 생각해 볼 수 있다.
dp[K][N] = dp[K-1][0] + dp[K-1][1] + ... + dp[K-1][N-1] + dp[K-1][N]
인데 dp[K-1][0] + dp[K-1][1] + ... + dp[K-1][N-1] = dp[K][N-1] 이라고 볼 수 있다.
즉, dp[K][N] = dp[K][N-1] + dp[K-1][N] 로 일반화 시킬 수 있다.

위의 알고리즘을 만들어보면 아래와 같다.
#include <iostream>
using namespace std;
int N,K;
long dp[201][201];
long DIV = 1000000000;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> N >> K;
for (int i = 1; i <= K; i++) dp[i][0] = 1;
for (int i = 0; i <= N; i++) dp[1][i] = 1;
for (int i = 1; i <= K; i++) {
for (int j = 1; j <= N; j++) {
long sum = dp[i][j-1] + dp[i-1][j];
dp[i][j] = sum % DIV;
}
}
cout << dp[K][N];
return 0;
}'코딩 테스트' 카테고리의 다른 글
| [백준] 1915번 - 가장 큰 정사각형 (4) | 2023.07.09 |
|---|---|
| [백준] 2240번 - 자두나무 (0) | 2022.10.01 |
| 백준 1937번 - 욕심쟁이 판다 (1) | 2022.08.30 |
| 백준 18223번 - 민준이와 마산 그리고 건우 (0) | 2022.05.24 |
| 백준 1854번 - K번째 최단경로 찾기 (0) | 2022.05.11 |
